• Кинематическое динамо (1) (Желиговский В.А.);
• Кинематическое динамо (2) (Желиговский В.А.);
• Идеальная магнитогидродинамика (Желиговский В.А.);
• Численные методы (Желиговский В.А.);
• Прогноз опасности сильных афтершоков (Шебалин П.Н.).
• Проверка результатов распознавания мест возможного возникновения сильных землетрясений (Горшков А.И.).

Кинематическое динамо (1)

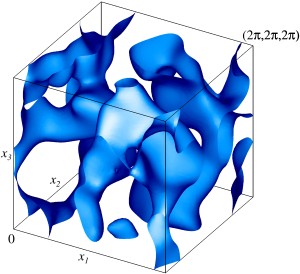
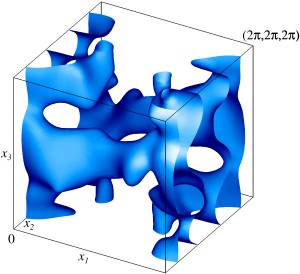
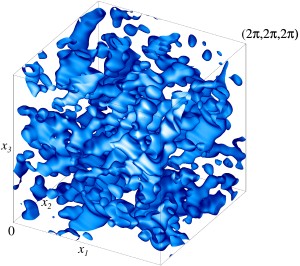
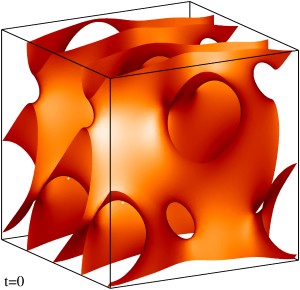
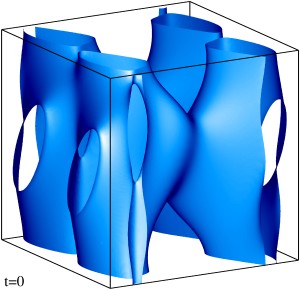
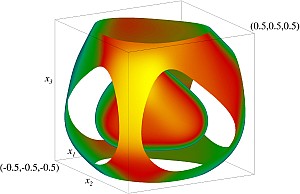
Магнитный α-эффект и вихревая диффузия не могут считаться основными механизмами генерации многомасштабных полей.

Рассмотрена кинематическая генерация пространственно-периодическим течением электропроводной жидкости магнитных мод вида произведения трехмерного поля, имеющего такую же периодичность, на гармонику Фурье с произвольным постоянным волновым вектором q. Проведены расчеты магнитных мод с максимальным по q инкрементом роста γ для модельного течения общего вида (в таких течениях присутствует магнитный α-эффект) и для центрально-симметричного модельного течения (в таких течениях α-эффект отсутствует, но в модельном течении присутствует отрицательная магнитная вихревая диффузия). Показано, что магнитные моды с максимальным по q инкрементом роста γ характеризуются слабым разделением пространственных масштабов, поэтому указанные эффекты не могут считаться основными механизмами их генерации.

Изоповерхности плотности кинетической энергии модельного течения общего вида на уровне 50% от максимальной плотности. Изображен один куб периодичности течения.

 а)   б) 

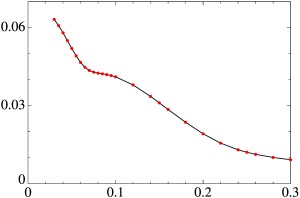
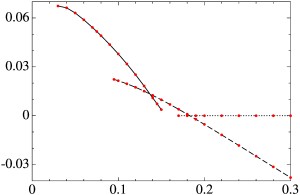
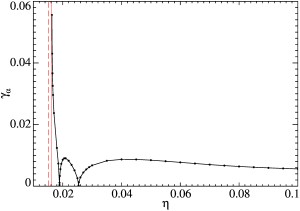
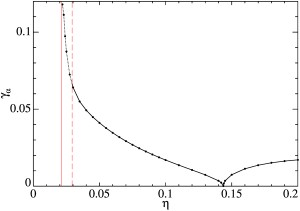
Максимальный по q инкремент роста магнитных мод γ (вертикальная ось) (а) для модельного течения общего вида и волновой вектор q (вертикальная ось) (б), для которого достигается max_qγ, как функции молекулярной магнитной диффузии η (горизонтальная ось). Точки показывают вычисленные величины max_qγ (а). Сплошная линия: |q|, штриховые: q_n, длина штриха увеличивается с индексом n (б).

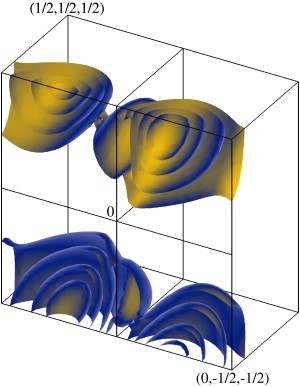
Изоповерхности инкремента γ в пространстве волновых векторов q для модельного течения общего вида для молекулярной магнитной диффузии η=0.1 на уровнях 25%, 50%, 75% и 90% от max_qγ.

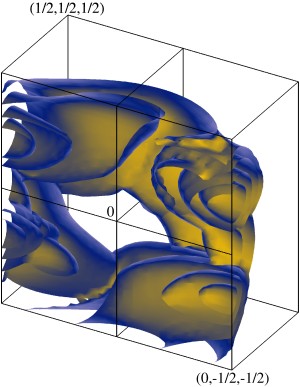
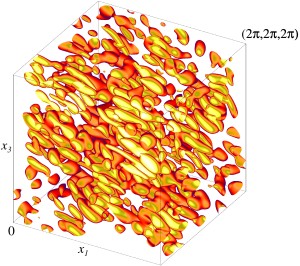
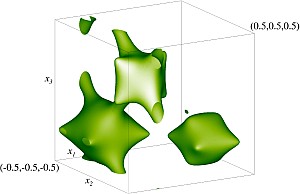
Изоповерхности плотности кинетической энергии центрально-симметричного модельного течения на уровне 60% от максимальной плотности. Изображен один куб периодичности течения.

 а)   б) 

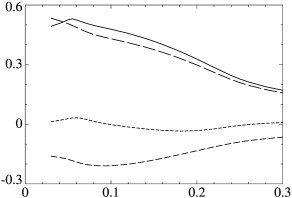
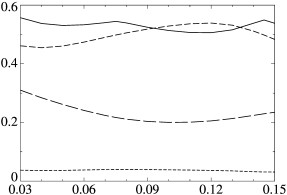
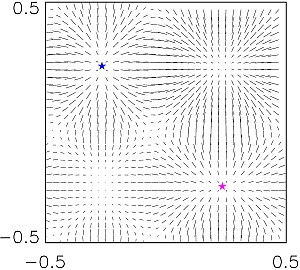
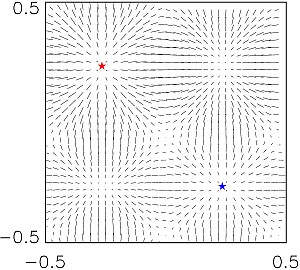
Максимальный по q инкремент роста магнитных мод g (вертикальная ось) (а) для центрально-симметричного модельного течения и волновой вектор q (вертикальная ось) (б), для которого достигается max_qγ, как функции молекулярной магнитной диффузии h (горизонтальная ось). Точки показывают вычисленные величины max_qγ (а). Локальные максимумы γ достигаются при q=0 (правая ветвь, пунктир, нейтральные моды), q=(0,1/2,0) (средняя ветвь, штриховая линия), для левой ветви (сплошная линия) соответствующие q изображены на графиках (б): сплошная линия: |q|, штриховые: q_n, длина штриха увеличивается с индексом n (б).

Изоповерхности инкремента роста γ магнитных мод в пространстве волновых векторов q для центрально-симметричного модельного течения общего вида для молекулярной магнитной диффузии η=0.1 на уровнях 25%, 50%, 75% и 90% от max_qγ.

В.А. Желиговский, Р.А. Чертовских. О кинематической генерации магнитных мод блоховского типа. Физика Земли, №1, 2020.

Кинематическое динамо (2)

Отсутствие спиральности у течения несжимаемой электропроводной жидкости не препятствует генерации коротко- или длинномасштабного магнитного поля и наличию у течения магнитного α-эффекта или отрицательной вихревой диффузии.
 
Построено 6 семейств трехмерных стационарных пространственно-периодических течений U несжимаемой электропроводной жидкости, плотность кинетической спиральности которых равна нулю: U rot U =0 в каждой точке пространства. Течения 4 семейств описаны замкнутыми формулами. Течения 4 семейств (другая четверка!) имеют нулевой спектр спиральности: Û_n(in×Û_n)=0 для всех n, где Û_n - коэффициенты Фурье поля скорости U, а черта обозначает комплексное сопряжение. Численно показано, что модельные течения пяти из этих семейств способны кинематически генерировать как коротко-, так и длинномасштабные магнитные поля, причем длинномасштабные - с помощью как магнитного α-эффекта, так и, для центрально-симметричных течений, отрицательной вихревой диффузии. Таким образом, спиральности полей (-Δ)^βU или (-Δ)^β rot U не контролируют способность соленоидального потока генерировать магнитное поле ни при каком действительном β (здесь Δ - оператор Лапласа).
 

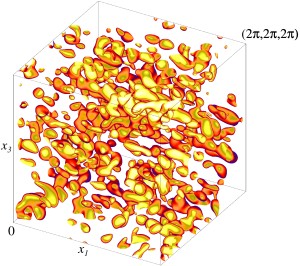
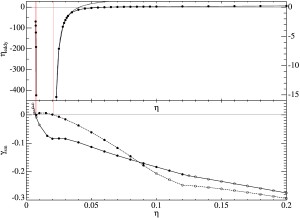
Изоповерхности величины скорости |U| (верхний ряд) и завихренности |rot U| (верхний ряд) для двух модельных течений семейства L с ненулевым спектром спиральности на уровне 1/3 соответствующего максимума, для которых генерация короткомасштабного поля начинается в четном (левый столбец) или нечетном (правый столбец) инвариантном подпространстве. Показан один куб периодичности течения.

Максимальный инкремент γ_α роста в медленном времени длинномасштабных магнитных полей, генерируемых магнитным α-эффектом в двух модельных течениях семейства L. Точки показывают вычисленные γ_α. Тонкие вертикальные линии расположены в критических η_crit начала генерации короткомасштабного магнитного поля в четном (сплошная линия) и нечетном (штриховая линия) инвариантном подпространстве; прерывистой линией на графике справа показаны инкременты γ_α в интервале между двумя η_crit, в котором генерация длинномасштабного магнитного поля магнитным α-эффектом скрыта на фоне более быстрой генерации короткомасштабного поля в нечетном инвариантном подпространстве. В точке η_crit в четном инвариантном подпространстве расположена вертикальная асимптота γ_α.

Изоповерхности поля скорости |U| (слева) и завихренности |rot U| (справа) для центрально-симметричного (и потому не обладающего α-эффектом) модельного течения семейства L с ненулевым спектром спиральности на уровнях 1/3 и 2/5 соответствующего максимума. Показан один куб периодичности течения.

Вверху: Минимальная магнитная вихревая диффузия η_eddy в модельном течении семейства L. Точки обозначают вычисленные η_eddy. Пунктирная линия - гипербола, найденная методом минимальных квадратов по 7 вычисленным величинам η_eddy в интервале 0.023≤η≤0.032. Внизу: доминирующие инкременты роста γ_sm короткомасштабных магнитных мод из центрально-симметричного (сплошная линия) и центрально-антисимметричного (штриховая линия) инвариантного подпространства, генерируемых этим течением. Темные (светлые) кружки обозначают, что соответствующие собственные значения оператора магнитной индукции действительны (комплексны). Тонкие вертикальные линии расположены в критических η_crit начала генерации короткомасштабных магнитных полей в двух указанных инвариантных подпространствах. В точках η_crit  начала генерации в инвариантных подпространствах, где действительное собственное значение проходит через 0, расположены вертикальные асимптоты η_eddy.

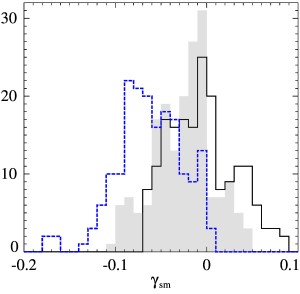
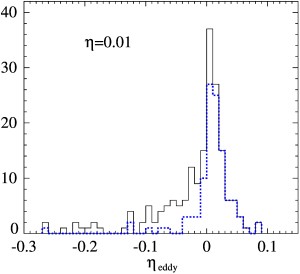
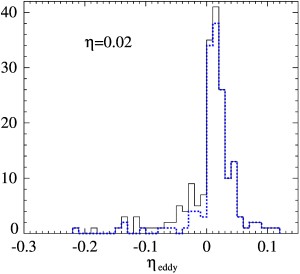
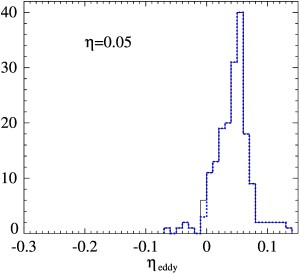
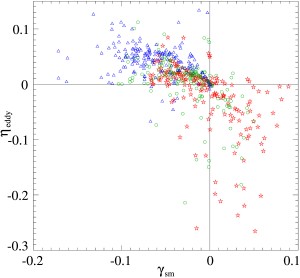
Течения семейства C ("косинусные течения") имеют компоненты
u₁ = n (b₁ sin(a⋅x) + a₁ sin(b⋅x)) cosnx₃,
u₂ = n (b₂ sin(a⋅x) + a₂ sin(b⋅x)) cosnx₃,
u₃ = -(a⋅b)(cos(a⋅x) + cos(b⋅x)) sinnx₃.
Было выделено 183 т.н. "основные" косинусные течения, в которых компоненты постоянных горизонтальных векторов a и b, а также волновое число n - целые числа от -3 до 3, и были наложены другие естественные условия - например, никакие два основные потока не переводятся друг в друга симметриями.

Совместное распределение минимальной магнитной вихревой диффузии η_eddy и доминирующих инкрементов роста γ_sm короткомасштабных магнитных мод среди основных течений семейства С для η = 0.01 (звездочки), 0.02 (кружки), 0.05 (треугольники).

Rasskazov A., Chertovskih R., Zheligovsky V. Magnetic field generation by pointwise zero-helicity three-dimensional steady flow of incompressible electrically conducting fluid. Phys. Rev. E, 97, 2018, 043201 [arxiv.org/abs/1708.08770].

Andrievsky A., Chertovskih R., Zheligovsky V. Pointwise vanishing velocity helicity of a flow does not preclude magnetic field generation. Phys. Rev. E, 99, 2019, 033204 [arxiv.org/abs/1811.00859].

Идеальная магнитогидродинамика

Разложение решения уравнений идеальной магнитогидродинамики в ряд Тейлора по времени может быть использовано для его вычисления.
 
Доказано, что, если начальные скорость течения жидкости и магнитное поле - аналитические функции пространственных переменных, то решение системы трехмерных уравнений идеальной магнитогидродинамики аналитично по пространственным переменным и времени на некотором временнóм интервале строго положительной длины. С использованием свойства вмороженности магнитного поля построены разложения решения в эйлеровых и лагранжевых координатах в ряды Тейлора по времени. Для их коэффициентов выведены рекуррентные соотношения. Эти результаты положены в основу алгоритмов численного интегрирования рассматриваемых уравнений по времени. Лагранжев алгоритм опробован в расчетах; в решении наблюдается образование структур меньших размерностей. Уже при t≈1.5 использованное пространственное разрешение 256³ гармоник Фурье оказывается недостаточным, и на изоповерхностях появляется численная "рябь".
 

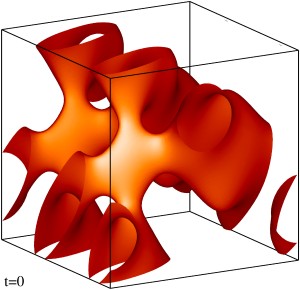
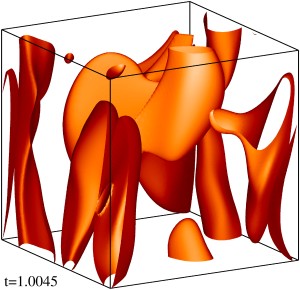
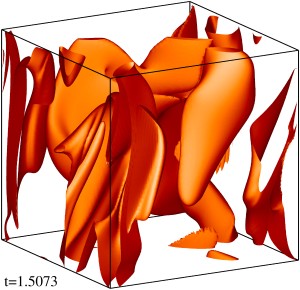
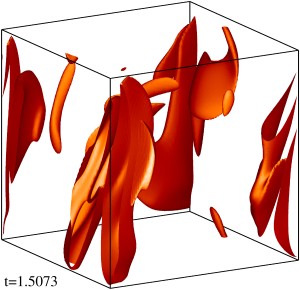
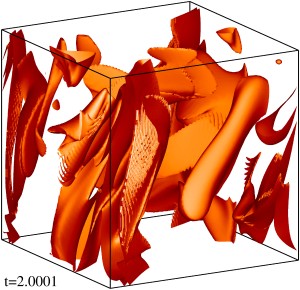
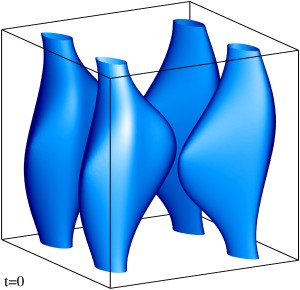
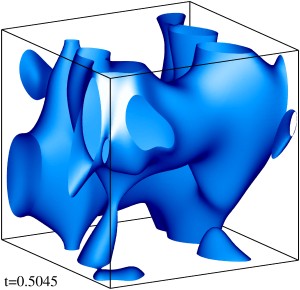
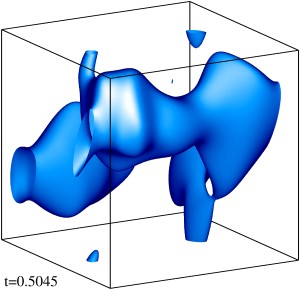
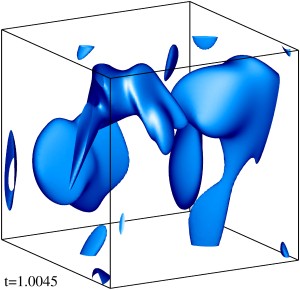
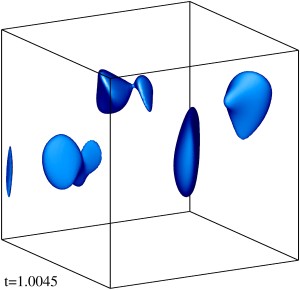
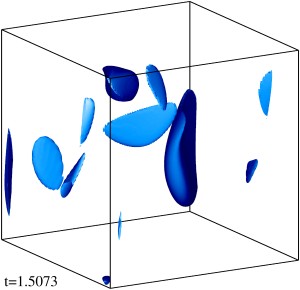
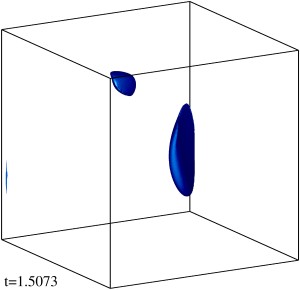
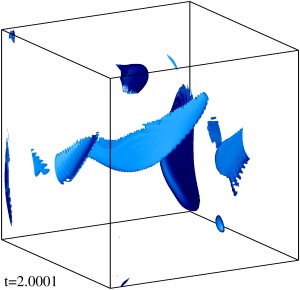
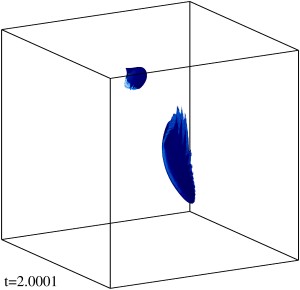
Изоповерхности плотности кинетической энергии течения на уровне 1/3 (левый столбец) и 1/2 (правый столбец) максимума с шагом по времени ≈0.5 (точные времена t указаны на рисунке). Изображен один куб периодичности течения.

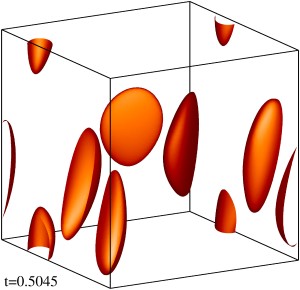
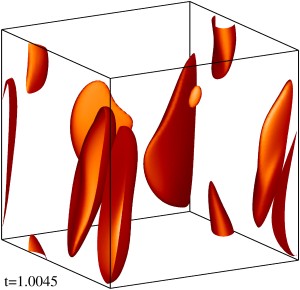
Изоповерхности плотности магнитной энергии течения на уровне 1/3 (левый столбец) и 1/2 (правый столбец) максимума с шагом по времени ≈0.5 (точные времена t указаны на рисунке). Изображен один куб периодичности течения.

В.А. Желиговский, О.М. Подвигина. Численный алгоритм интегрирования по времени задач идеальной магнитогидродинамики, опирающийся на аналитичность их решений. Физика Земли, №1, 2020.

Численные методы

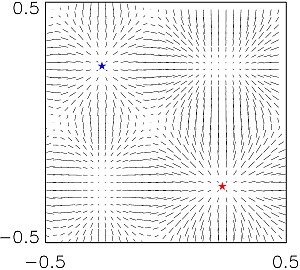
Создан метод вычисления решения уравнения Монжа-Ампера с контрастной правой частью.
 
В космологии считается, что после отделения фотонов от вещества через 380 тысяч лет после Большого Взрыва распределение вещества было равномерным с точностью порядка 10^-5-10^-6 от средней плотности. Этой флюктуации оказалось достаточно, чтобы под действием гравитации распределение вещества во Вселенной стало крайне неравномерным - таким, каким мы его наблюдаем. Поскольку гравитация - потенциальная сила, на пространственных масштабах, существенно бóльших размеров галактик, перемещение вещества описывается градиентом решения т.н. уравнения Монжа-Ампера: det(∂²u/∂x_i∂x_j) = r(x), где правая часть r - плотность вещества во Вселенной в нашу эпоху. Если всюду r>0, то для стандартных краевых условий данное уравнение имеет единственное решение, но эта теорема может нарушаться уже при r³0. Это приводит к вычислительным сложностям при большой величине параметра контраста задачи r_max/r_min (что характерно для задач астрофизики). Если r - пространственно-периодическая функция, то u = u' + c|x|², где u' имеет такую же периодичность, c = <r>/2, а угловые скобки обозначают усреднение по ячейке периодичности.
 
Метод предполагает последовательное вычисление решений регуляризованных уравнений и их экстраполяцию по параметру регуляризации. Он был применен для модельного распределения вещества по трем "галактикам" в кубе периодичности [-1/2,1/2]³ с гауссовым распределением вещества каждой "галактики". Параметр контраста задачи ~10⁷.

Слева: изоповерхности решения u для модельной задачи на уровнях 1/2 и 1/8 максимума u. Справа: изоповерхность Δu' (лапласиана u') на уровне 1/3 максимума. Модельные "галактики" находятся внутри показанных структур. Показан куб периодичности распределения r.

∇u' на плоскостях, параллельных координатным, проходящих через три модельные "галактики", положение которых показано звездами. Цвет кодирует массы галактик: синий, фиолетовый, красный, в порядке возрастания масс.

Zheligovsky V., Podvigina O., Frisch U. The Monge-Ampère equation: various forms and numerical methods. J. Computational Physics, 229, 2010, 5043-5061 [arxiv.org/abs/0910.1301].

Прогноз опасности сильных афтершоков

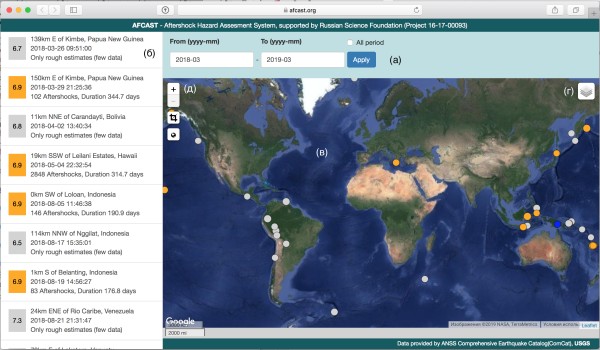
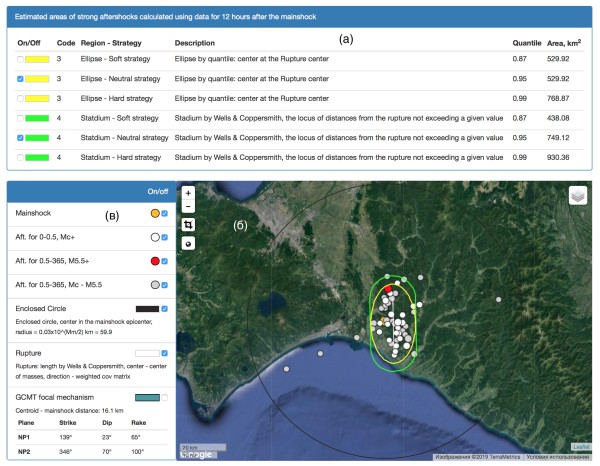
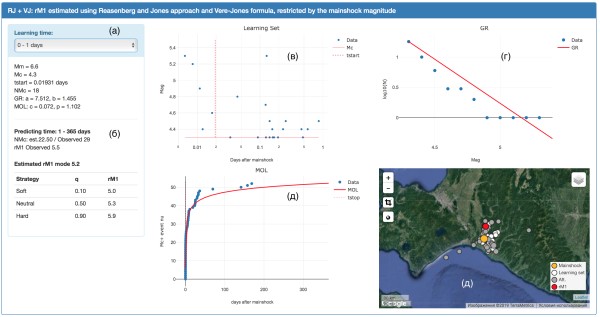
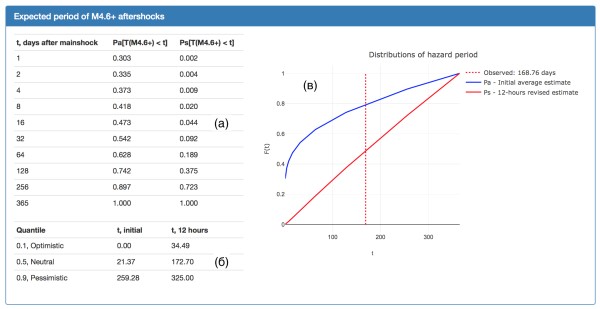
В рамках проекта РНФ 15-17-00093 в ИТПЗ РАН под руководством д.ф.-м.н. П.Н. Шебалина была разработана Информационная система автоматической оценки сейсмической опасности после сильных землетрясений AFCAST. Эта система работает в режиме времени близком к реальному. Оцениваются область эпицентров ожидаемых афтершоков, максимальная магнитуда и длительность опасного периода.  Для оценки используются данные каталога ANSS ComCat Геологической службы США (USGS). В настоящее время ведется прогноз возможных афтершоков землетрясений мира магнитудой 6.5 и более.
 
При создании системы был получен ряд фундаментальных результатов. В частности, была продемонстрирована независимость магнитуды сильных афтершоков от времени [Баранов, Шебалин, 2019]. Было введено понятие продуктивности землетрясения относительной магнитуды (число инициированных непосредственно этим землетрясением событий магнитудой не ниже порога, определяемого фиксированной разностью относительно этого землетрясения). Установлено, что это величина имеет экспоненциальное распределение, а среднее значение распределения быстро убывает с глубиной очага. Экспоненциальное распределение числа афтершоков относительной магнитуды объясняет форму распределения разности магнитуды основного толчка и сильнейшего афтершока (закон Бота). Размах (дисперсия) этого распределения определяется значением параметра b закона Гутенберга-Рихтера, а положение моды распределения средним значением числа афтершоков относительной магнитуды. Это позволяет также оценить зависимость разности магнитуды основного толчка и сильнейшего афтершока от времени.
 
Для работы с системой AFCAST перейдите по ссылке https://afcast.org/afcast/. Краткая инструкция по работе с системой AFCAST находится по ссылке: AFCAST-manual.pdf.
Результаты системы носят предварительный характер и могут использоваться только в научных целях. В случае неполадок каких-либо элементов системы AFCAST необходимо сообщить по e-mail: bars.vl@gmail.com, vadim@krsc.ru.
 

Примеры работы программы

Баранов С.В., Шебалин П.Н. О прогнозировании афтершоковой активности. 2. Оценка области распространения сильных афтершоков // Физика Земли. 2017. №  3. С.  43–61.

Шебалин П.Н., Баранов С.В. Экспресс оценка опасности сильных афтершоков района Камчатки и?Курильских островов // Вулканология и сейсмология. 2017. №  4. С.  57

Shebalin P., Baranov S. Long-Delayed Aftershocks in New Zealand and the 2016 M7.8 Kaikoura Earthquake  // Pure and Applied Geophysics. 2017. V. 174, No. 7, P. 3751–3764. DOI 10.1007/s00024-017-1608-9.

Shebalin P., Narteau C. Depth dependent stress revealed by aftershocks // Nature Communiations. 2017. V. 8, No. 1317. DOI: 10.1038/s41467-017-01446-y

Баранов С.В., Шебалин П.Н. О прогнозировании афтершоковой активности. 3. Динамический закон Бота // Физика Земли. 2018. Т. 54. №6. С. 129-136.

Шебалин П. Математические методы анализа и прогноза афтершоков землетрясении?: необходимость смены парадигмы // Чебышевский сборник. 2018. Т. XIX, Вып. 4(68). С. 227-242.

Шебалин П.Н., Баранов СВ., Дзебоев  Б.А. Закон повторяемости количества афтершоков // Доклады Академии наук. 2018. T. 481. № 3.

Баранов С.В., Шебалин П.Н. Глобальная статистика афтершоков сильных землетрясений: независимость времен и магнитуд // Вулканология и сейсмология. 2019. №2. С. 67-76.

Баранов С.В., Павленко В.А., Шебалин П.Н. О прогнозировании афтершоковой активности. 4. Оценка максимальной магнитуды последующих афтершоков // Физика Земли. 2019. Т. 55. №4. С. 1-11.

Баранов С.В., Шебалин П.Н. О прогнозировании афтершоковой активности. 5. Оценка длительности опасного периода // Физика Земли. 2018. Т. 55. №5.

Проверка результатов распознавания мест возможного возникновения сильных землетрясений

В 1972 г. В.И. Кейлис-Борок и И.М. Гельфанд предложили феноменологический подход к идентификации сейсмоопасных зон, основанный на морфоструктурном районировании и распознавании образов. Методология позволяет определять сейсмогенные узлы, в которых возможно возникновение  сильных землетрясений по комплексу  геологических, геоморфологических и геофизических признаков, которые не содержат информации об известной  сейсмичности изучаемого региона. В период 1972-2018 годов было изучено в общей сложности 26 сейсмоактивных регионов мира (Табл. 1) и опубликованы карты, показывающие положение распознанных сейсмоопасных узлов в каждом регионе. Впоследствии в 11 из этих регионов произошли землетрясения соответствующих магнитуд. Был проведен анализ корреляции пост-публикационных событий соответствующих магнитуд с распознанными ранее сейсмогенными узлами. Тест был выполнен с использованием каталога землетрясений NEIC, поскольку он с одинаковой точностью определяет местоположение и магнитуды землетрясений по всему миру. Было установлено, что 86% таких событий (Табл 2) и Рис. 1-2 произошли в распознанных сейсмогенныхе узлах. Проведенный анализ демонстрирует достаточную эффективность и надежность методики распознавания сейсмогенных узлов и подтверждает в целом гипотезу о связи сильных землетрясений с узлами.

На Рис. 1-2 представлены примеры корреляции пост-публикационных землетрясений с распознанными высокосейсмичными узлами на Памире и Тянь-Шане и на Большом Кавказе.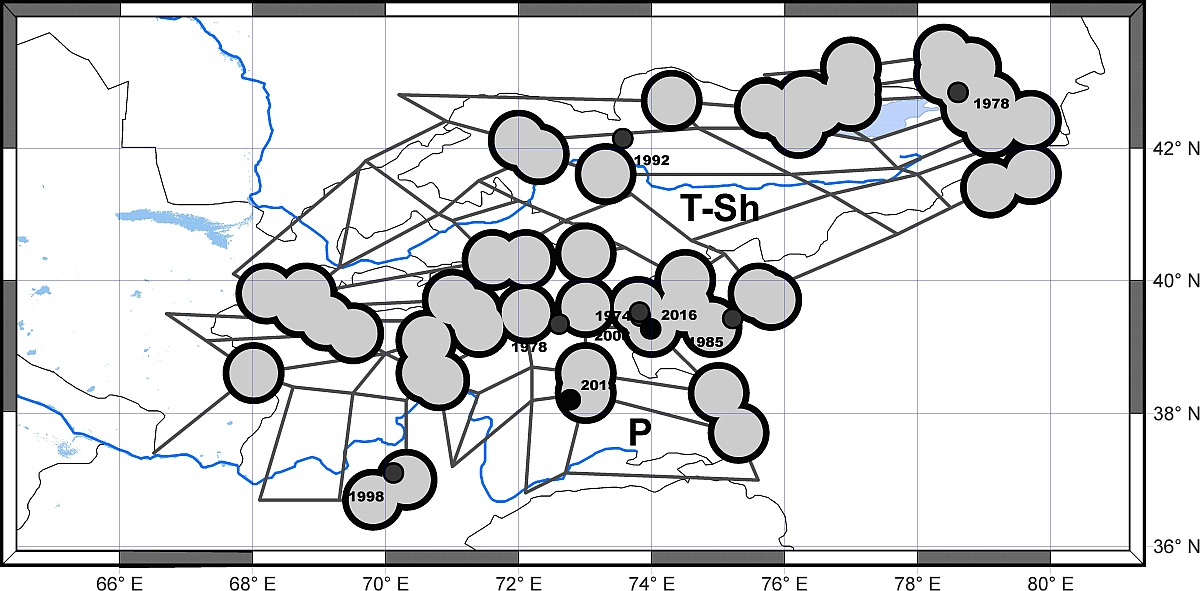

Рис. 1. Сейсмогенные узлы, распознанные в Памире (Р) и Тянь-Шане (T-Sh) (Gelfand et al., 1972) и их корреляция с пост-публикационными событиями M6.5+.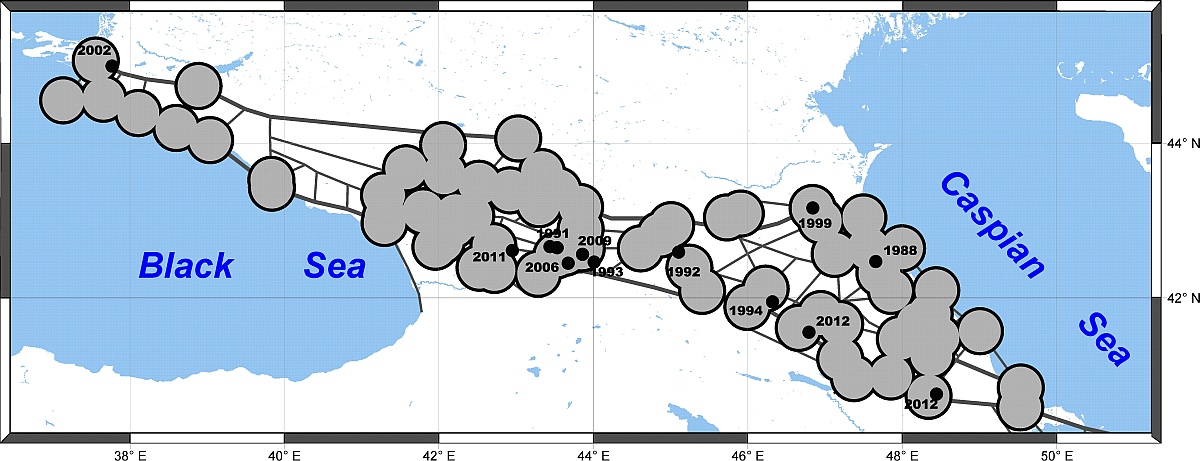

Рис. 2. Сейсмогенные узлы, распознанные на Большом ( Gvishisni et al., 1988) и их корреляция с пост-публикационными землетрясениями 5+. В этом регионе все пост-публикационные события коррелируют с распознанными сейсмогенными узлами.

Примечания: М₀ – пороговая магнитуда землетрясений, для которой проводилось распознавание в данном регионе; В* - узлы, распознанные как высокосейсмичные, но на момент решения задачи землетрясения с М ≥ М₀ в них не были зарегистрированы; Н - узлы, распознанные как низкосейсмичные.

Таблица 2 показывает, что 89 (около 86%) событий произошли в узлах, распознанных как В. Классификация узлов на В и Н с помощью алгоритма распознавания нетривиальна. Вероятность ошибки данной классификации может быть оценена как отношение числа событий, произошедших в узлах Н к общему числу событий (4/104 = 3.7%). Эта малая величина свидетельствует о достаточной надежности и статистической значимости результатов распознавания.

Gorshkov A., Novikova O. (2018) Estimating the validity of the recognition results of earthquake prone areas using the ArcMap. Acta Geophysica. Volume 66, Issue 5, pp 843-853. Doi 10.1007/s11600-018-0177-3